Voralgebra-Arbeitsblätter zum Schreiben von Ausdrücken

von 05

Arbeitsblatt für algebraische Ausdrücke 1

Schreiben Sie die Gleichung oder den Ausdruck algebraisch.

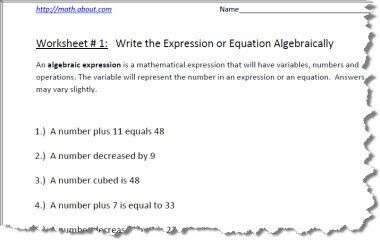
Drucken Sie das PDF-Arbeitsblatt oben aus. Die Antworten finden Sie auf der zweiten Seite.

Ein algebraischer Ausdruck ist ein mathematischer Ausdruck, der Variablen, Zahlen und Operationen enthält. Die Variable repräsentiert die Zahl in einem Ausdruck oder einer Gleichung. Die Antworten können leicht variieren. Die Fähigkeit, Ausdrücke oder Gleichungen algebraisch zu schreiben, ist ein Voralgebra-Konzept, das vor der Aufnahme erforderlich ist Algebra.

Die folgenden Vorkenntnisse sind erforderlich, bevor Sie diese Arbeitsblätter erstellen:

Ein Verständnis, dass eine Variable ein Buchstabe wie x, y oder n ist und die unbekannte Zahl darstellt.

Dass ein Ausdruck eine Aussage in der Mathematik ist, die kein Gleichheitszeichen enthält, aber Zahlen, Variablen und Operationszeichen wie +, - x usw. enthalten kann. Zum Beispiel ist 3y ein Ausdruck.

Dass eine Gleichung eine Aussage in der Mathematik ist, die ein Gleichheitszeichen enthält.

instagram viewer

Es sollte eine gewisse Vertrautheit mit geben ganze Zahlen Das sind ganze Zahlen oder ganze Zahlen mit einem negativen Vorzeichen.

Es ist auch wichtig, die Begriffe zu verstehen und zu kennen: Quotient, Produkt, Summe, erhöht und verringert, wenn sie sich auf Operationen beziehen. Wenn beispielsweise die Wortsumme verwendet wird, müssen Sie wissen, dass die Operation das Hinzufügen oder Verwenden des + -Zeichens umfasst. Wenn der Wortquotient verwendet wird, bezieht er sich auf das Teilungszeichen, und wenn das Wort Produkt verwendet wird, bezieht er sich auf das Multiplikationszeichen, das durch a angegeben ist. oder indem Sie die Variable wie in 4n neben die Zahl setzen, was 4 x n bedeutet

von 05

Arbeitsblatt zum algebraischen Ausdruck 2

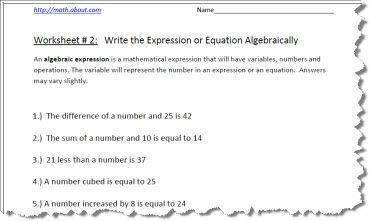
Arbeitsblätter für algebraische Ausdrücke # 2 — Arbeitsblatt zum algebraischen Ausdruck 2 von 5.D. D. Russell

Schreiben Sie die Gleichung oder den Ausdruck algebraisch.

Drucken Sie das PDF-Arbeitsblatt oben aus. Die Antworten finden Sie auf der zweiten Seite.

Das Ausschreiben der algebraischen Ausdrücke oder Gleichungen und das Erlernen der Vertrautheit mit dem Prozess ist eine Schlüsselkompetenz, die erforderlich ist, um algebraische Gleichungen zu vereinfachen. Es ist wichtig, die zu verwenden. Wenn Sie sich auf die Multiplikation beziehen, möchten Sie die Multiplikation nicht mit x der Variablen verwechseln. Obwohl die Antworten auf der zweiten Seite des PDF-Arbeitsblatts angegeben sind, können sie je nach dem Buchstaben, der zur Darstellung des Unbekannten verwendet wird, geringfügig variieren. Wenn Sie Aussagen sehen wie:
Eine Zahl mal fünf ist einhundertzwanzig, anstatt n x 5 = 120 zu schreiben, würden Sie 5n = 120 schreiben, 5n bedeutet, eine Zahl mit 5 zu multiplizieren.

von 05

Arbeitsblatt zum algebraischen Ausdruck 3

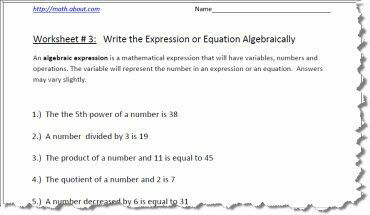
Arbeitsblatt zum algebraischen Ausdruck Nr. 3.D. D. Russell

Schreiben Sie die Gleichung oder den Ausdruck algebraisch.

Drucken Sie das PDF-Arbeitsblatt oben aus. Die Antworten finden Sie auf der zweiten Seite.

Algebraische Ausdrücke sind bereits in der 7. Klasse im Lehrplan erforderlich. Die Grundlagen für die Durchführung der Aufgaben liegen jedoch in der 6. Klasse. Algebraisches Denken geschieht mit der Verwendung der Sprache des Unbekannten und der Darstellung des Unbekannten mit einem Buchstaben. Wenn Sie eine Frage stellen wie: Der Unterschied zwischen einer Zahl und 25 beträgt 42. Der Unterschied sollte bedeuten, dass Subtraktion impliziert ist und dass die Aussage dann wie folgt aussehen würde: n - 24 = 42. Mit der Übung wird es zur zweiten Natur!

Ich hatte einen Lehrer, der mir einmal sagte, erinnere dich an die Regel von 7 und besuche sie erneut. Er meinte, wenn Sie sieben Arbeitsblätter ausführen und das Konzept erneut besuchen würden, könnten Sie behaupten, Sie wären am Punkt des Verstehens. Bisher scheint es funktioniert zu haben.